Lecture 7: Deadlock
starvation vs Deadlock
- Starvation vs. Deadlock
- Starvation: thread waits indefinitely(无限期的)
- Low-priority thread waiting for resources constantly in use by high-priority thread
- Deadlock: circular waiting for resources
- Thread A owns Res 1 and is waiting for Res 2
- Thread B owns Res 2 and is waiting for Res 1
- Starvation: thread waits indefinitely(无限期的)
Conditions for Deadlock
- Deadlock not always deterministic
- Deadlocks occur with multiple resources
- Means you cannot decompose the problem
- Cannot solve deadlock for each resource independently
- System with 2 disk drives and two threads
- Each thread needs 2 disk drives to function
- Each gets one disk and waits for another one
Four requirements for Deadlock
- Mutual exclusion
- Only one thread at a time can use a resource
- Hold and wait
- Thread holding at least one resource is waiting to acquire additional resource held by other threads
- No preemption
- Resources are released only voluntarily by the thread holding the resource, after thread is finished with it
- Circular wait
- There exists a set {T_1, ..., T_n} of waiting threads
- T1 is waiting for a resource that is held by T2
- T2 is waiting for a resource that is held by T3
- ...
- Tn is waiting for a resource that is held by T1
- There exists a set {T_1, ..., T_n} of waiting threads
Resource-Allocation Graph
- System Model
- A set of Threads T1, T2, ... Tn
- Resource types R1,R2,...,Rm
- CPU cycles, memory space, I/O devices
- Each resource type R1 has W1 instances
- Each thread utilizes a resources as follows:
Request(),Use(),Release()
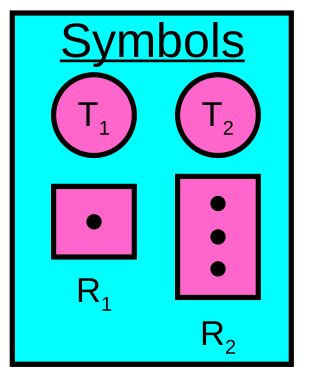
- Resource-Allocation Graph:
- V is partitioned into two types:
- T = {T1,T2,...,Tn}, the set threads in the system
- R = {R1,R2,...,Rm}, the set of resource types in system
- Request edge - directed edge - T1 -> Rj
- assignment edge - directed edge Rj -> Ti
- V is partitioned into two types:
Resource Allocation Graph Examples
- Recall:
- request edge - directed edge T1 -> Rj
- assignment edge - directed edge Rj -> Ti

Methods for Handling Deadlocks
- Allow system to enter deadlock and then recover
- Requires deadlock detection algorithm
- Some technique for forcibly preempting resources and/or terminating tasks
- Ensure that system will never enter a deadlock
- Need to monitor all resource acquisitions
- Selectively deny those that might lead to deadlock
- Ignore the problem and pretend that deadlocks never occur in the system
- Used by most operating system, including UNIX
Deadlock Detection Algorithm
- Only one of each type of resource -> look for cycles
- More than one resource of each type
- More deadlock detection algorithm
Several Instances of a Resource Type
Available: A vector of length m indicates the number of available resources of each typeAllocation: A n * m matrix defines the number of resources of each type currently allocated to each process.Request: An n * m matrix indicates the current request of each process. If Request[i_j]=k, then process P_i is requesting k more instances of resource type. R_j.
Detection Algorithm
- Let
WorkandFinishbe vectors of length m and n, respectly initialize:- Work = Available
- For i = 1,2,...n, if Allocation_i not 0, then Finish[i] = false; otherwise, Finish[i] = true.
- Find an index i such that both:
- Finish[i] == false
- Request_i <= Work
- If no such i exists, go to step 4
- As follow.
- Work = Work + Allocation_i
- Finish[i] = true
- go to step 2
- If Finish[i] == false, for some i, 1 <= i <= n, then the system is in deadlock state. Moreover, if Finish[i] == false, then P_i is deadlocked
Example of Detection Algorithm
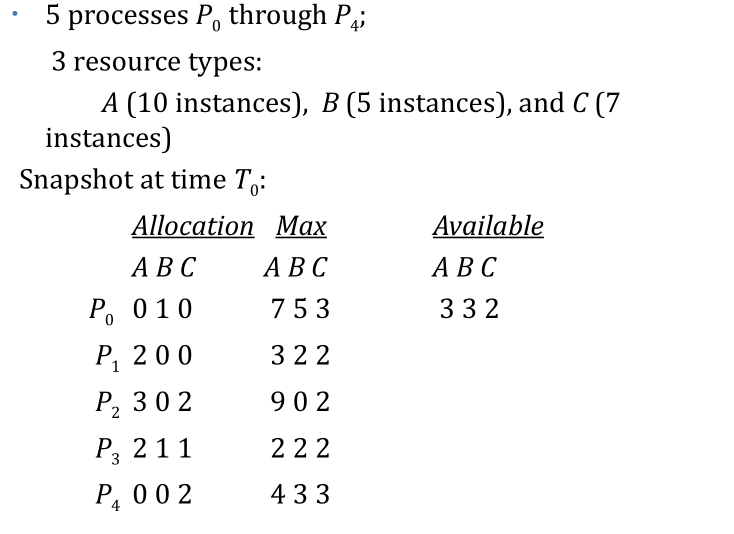
- Five processes P_0 through P_4; three resource type A(7 instances), B(2 instances), and C(6 instances)
- Snapshot at time T_0:
Allocation
| A | B | C | |
|---|---|---|---|
| P0 | 0 | 0 | 0 |
| P1 | 2 | 0 | 0 |
| P2 | 3 | 0 | 3 |
| P3 | 2 | 1 | 1 |
| P4 | 0 | 0 | 2 |
Request
| A | B | C | |
|---|---|---|---|
| P0 | 0 | 0 | 0 |
| P1 | 2 | 0 | 2 |
| P2 | 0 | 0 | 0 |
| P3 | 1 | 0 | 0 |
| P4 | 0 | 0 | 2 |
Available
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
Sequence <P_0,P_2,P_3,P_1,P_4> will result in Finish[i] = true for all i.
If P_2 request an additional instance of type C, that is
Request
| A | B | C | |
|---|---|---|---|
| P0 | 0 | 0 | 0 |
| P1 | 2 | 0 | 2 |
| P2 | 0 | 0 | 0 |
| P3 | 1 | 0 | 0 |
| P4 | 0 | 0 | 2 |
The state of system:
- Can reclaim resources held by process P_0(not deadlocked), but insufficient resources to fulfill other process; request
- Deadlock exist, consisting of processes P_1, P_2, P_3, and P_4
What to do when detect deadlock?
- Terminate thread, force it to give up resources
- In Bridge example, Godzilla picks up a car, hurls it into the river. Deadlock solved!
- Shoot a dining philosopher
- But, ont always possible
- Preempt resources without killing off thread
- Take away resources from thread temporarily
- Does not always fit with semantics of computation
- Roll back actions of deadlocked threads
- For bridge example, make one car roll backwards(may require others behind him)
- Common technique in databases(transactions)
- Of courses, if you restart in exactly the same way, may reenter deadlock once again
- Many operating systems use other options
Techniques for Preventing Deadlock
- Infinite resources
- Include enough resources so that no one ever runs out of resources. Examples:
- Bay bridge with 12,000 lanes. Never wait!
- Infinite disk space (not realistic yet?)
- Include enough resources so that no one ever runs out of resources. Examples:
- No sharing of resources(totally independent threads)
- Not very realistic
- Do not allow waiting
- Technique used in Ethernet/some multiprocessor nets
- Every speaks at once. On collision, back off and retry
- Inefficient, since have to keep retrying
- Consider: driving to SUSTech; when hit traffic jam, suddenly you are transported back home and told to retry!
- Technique used in Ethernet/some multiprocessor nets
- Make all threads request everything they will need at the beginning
- Problem: Predicting future is hard, tend to over-estimate resources. Example:
- If need 2 chopsticks, request both at same time
- Don not leave home until we know no one is using any intersection between home and SUSTech; only one car on the Bay Bridge at a time
- Problem: Predicting future is hard, tend to over-estimate resources. Example:
- Force all threads to request resources in a particular order preventing any cyclic use of resources
- Thus, preventing deadlock
- Example (x.P, y.P, z.P,…)
- Make tasks request disk, then memory, then…
- Keep from deadlock on freeways around SF by requiring everyone to go clockwise
Banker's Algorithm
- Multiple instances of each resource type
- Each process must a priori claim maximum use
- When a process requests a resource it may have to wait
- When a process gets all its resources it must return them in a finite amount of time
Data Structures for the Banker's Algorithm
Let n = number of processes, and m = number of resources type
- Available: Vector of length m. If available [j] = k, there are k instances of resource type Rj available
- Max: n x m matrix. If Max [i,j] = k, then process Pi may request at most k instances of resource type Rj
- Allocation: n x m matrix. If Allocation[i,j] = k then Pi is currently allocated k instances of Rj
- Need: n x m matrix. If Need[i,j] = k, then Pi may need k more instances of Rj to complete its task
Need [i,j] = Max[i,j] – Allocation [i,j]
Safety Algorithm
1.Let Work and Finish be vectors of length m and n ,respectively. Initialize:
- Work = Available
- Finish [i] = false for i = 0, 1, …, n- 1
2.Find an index i such that both:
- Finish [i] = false
- Need[i] <= Work (i.e., for all k, Need[i,k] <= Work[k])
3.Work = Work + Allocation[i]
- Finish[i] = true
- go to step 2
4.If Finish [i] == true for all i, then the system is in a safe state
Resource-Request Algorithm for Process Pi
Request = request vector for process P_i. If Request [i,j] = k then process P_i wants k instances of resource type R_j
1.If Request[i] <= Need[i] go to step 2. Otherwise, raise error condition, since process has exceeded its maximum claim.
2.If Request[i] <= Available, go to step 3. Otherwise P_i must wait, since resources are not available
3.Pretend to allocate requested resources to P_i by modifying the state as follows:
- Available = Available – Request;
- Allocation[i] = Allocation[i] + Request[i];
- Need[i] = Need[i] – Request[i];
If safe -> the resources are allocated to P_i
If unsafe -> P_i must wait, and the old resource-allocation state is restored
Example of Banker’s Algorithm